A biblioteca PyMunk é uma engine de simulação Física para Python muito interessante! Ela é perfeita para simular corpos rígidos em 2D e suas interações, como colisões.

Neste post irei aliar ela à pyglet (biblioteca para criação de jogos e aplicações visuais) para demonstrar como criar a simulação de um Pêndulo Simples interativo.

O primeiro passo é instalar as dependências. Para isso, criamos um novo ambiente virtual (estou utilizando a versão 3.10.8 do Python):

$ python -m venv venv --prompt pendulum
$ source venv/bin/activate

(pendulum)$ pip install pyglet==1.5.27 pymunk==6.2.1

Iremos criar um modulo chamado simple_pendulum.py e começar por importar as bibliotecas:

import pymunk
import pyglet

from pyglet.window import key
from pymunk import Vec2d
from pymunk.pyglet_util import DrawOptions

Como base mínima deste programa, iremos declarar uma nova classe que herda de pyglet.window.Window e executá-la como uma app do Pyglet.

A classe Window aceita alguns argumentos para ajustar parâmetros da tela. Como utilizaremos parâmetros fixos neste exemplo, sobrescrevemos o __init__ e invocamos o __init__ do super(), passando estes parâmetros que vêm dos atributos de classe.

class SimulationWindow(pyglet.window.Window):
    CAPTION = "Fixed Pendulum Simulation."

    WIDTH = 720
    HEIGHT = 720

    INTERVAL = 1.0 / 100  # 100 updates / second

    FONT_SIZE = 16
    FONT_COLOR = (255, 255, 255, 255)

    def __init__(self):
        super().__init__(
            width=self.WIDTH, height=self.HEIGHT, caption=self.CAPTION
        )


if __name__ == "__main__":
    SimulationWindow()
    pyglet.app.run()

Executar este módulo deve abrir uma nova janela vazia:

Na sequência, expandimos o __init__ para criar uma nova instância da classe pymunk.Space.

    def __init__(self):
        super().__init__(
            width=self.WIDTH, height=self.HEIGHT, caption=self.CAPTION
        )

        self.space = pymunk.Space()
        self.space.gravity = Vec2d(0, -9807)  # mm/s²

O Espaços são a unidade básica de simulação. Os corpos (bodies), formas (shapes) e junções (joints ou constraints) são adicionados ao espaço e estes todos são simulados em conjunto, ao longo do tempo.

Após instanciar o espaço, aproveitamos e já definimos a gravidade utilizada na simulação, que é tratada como uma aceleração comum a todos os corpos.

Note que é utilizada uma instância de Vec2d. Esta é uma classe da própria pymunk para representar Vetores 2D, no formato Vec2d(x, y). Neste caso, há somente uma componente vertical para esta aceleração, apontando para baixo (negativa), com valor de 9807 mm/s², equivalente a aceleração da gravidade na Terra.

Vale comentar aqui que a biblioteca pymunk é agnostica em relação a unidades físicas! Não interessa para ela qual unidade está utilizando em suas medidas; Se passar um valor em s para uma função que espera tempo e um valor em mm para uma função de distância ou posição, então todos os cálculos serão feitos nestas unidades.

Unidades derivadas, como velocidade e aceleração, são calculadas a partir da combinação das outras unidades.

A gravidade foi definida em mm/s² já que definiremos posições e distâncias em mm.

Na sequência iremos construir nosso modelo e definir os corpos e formas que o compõem. Começamos por criar uma nova classe:

class Pendulum:
    MASS = 0.100  # g
    FORCE = 10  # mN

    def __init__(self, space: pymunk.Space):
        self.space = space

        self._create_entities()

Definimos as constantes MASS e FORCE que utilizaremos na sequência e no __init__ recebemos a instância de Space utilizada na simulação.

Invocamos o método privado _create_entities, onde iremos criar as entidades do modelo:

    def _create_entities(self) -> None:
        self.static_body = pymunk.Body(body_type=pymunk.Body.STATIC)
        self.static_body.position = (360, 360)

        moment = pymunk.moment_for_circle(
            mass=self.MASS, inner_radius=0, outer_radius=10.0
        )
        self.circle_body = pymunk.Body(mass=self.MASS, moment=moment)
        self.circle_body.position = (360, 50)

        circle_shape = pymunk.Circle(body=self.circle_body, radius=10.0)

        rod_joint = pymunk.constraints.PinJoint(
            a=self.static_body,
            b=self.circle_body,
        )

        self.space.add(
            self.static_body, self.circle_body, circle_shape, rod_joint
        )

A primeira entidade é chamada static_body, ou “corpo estático”. Se trata de um ponto fixo no espaço, onde iremos fixar nosso pêndulo.

A classe pymunk.Body é um dos conceitos básicos da biblioteca. Ela contêm todas as propriedades físicas do objetos (massa, posição, rotação, velocidade, etc…). No entanto, ela não define uma forma por si só.

Este ponto é definido na posição (360, 360), bem no centro da tela (considerando as constantes WIDTH e HEIGHT, definidas em SimulationWindow). Para que tenhamos uma simulação em mm, podemos assumir uma equivalência de 1:1 entre px e mm.

Na sequência, definimos o corpo para o Círculo que ficará na ponta do pêndulo. Antes de instanciar pymunk.Body para ele, é necessário calcular o momento de inercia, um dos argumentos necessários para se criar um corpo dinâmico, através da função pymunk.moment_for_circle.

Diferente do corpo estático, não passamos um valor de body_type para o círculo porque, por padrão, os corpos são criados com o tipo pymunk.Body.DYNAMIC.

Desta vez, também criamos uma instância da classe pymunk.Circle, subclasse de pymunk.Shape. Esta irá criar uma forma de um círculo, associado ao corpo que criamos anteriormente.

A principal utilidade das Shapes no PyMunk é realizar cálculo de colisões. Isso não será tão importante para nossa simulação, porém também é utilizada para gerar os gráficos (sprites) que serão utilizados no Pyglet.

E finalmente definimos uma pymunk.constraints.PinJoint entre o static_body e o circle_body.

Constraints são entidades utilizadas para restringir o movimento/comportamento dos corpos físicos. Existem diversas constraints, cada uma com um comportamento diferente.

A PinJoint, em específico, mantêm uma distância constante entre 2 objetos, e é utilizada para formar a haste de nosso pêndulo.

Para mais informações, consultar a referência.

Com todas as entidades criadas, utilizamos space.add para adicionar elas ao nosso espaço simulado.

Com a classe Pendulum definida, podemos continuar com a SimulationWindow:

    def __init__(self):
        super().__init__(
            width=self.WIDTH, height=self.HEIGHT, caption=self.CAPTION
        )

        self.space = pymunk.Space()
        self.space.gravity = Vec2d(0, -9807)  # mm/s²

        self.model = Pendulum(space=self.space)

        self.draw_options = DrawOptions()
        self.keyboard = key.KeyStateHandler()
        self.push_handlers(self.keyboard)

        pyglet.clock.schedule_interval(self.update, interval=self.INTERVAL)

A biblioteca pymunk possui alguns módulos utilitários para facilitar a visualização de suas entidades em outras bibliotecas, como pygame, matplotlib e, mais relevante ao nosso caso, pyglet. No início do programa, importamos a classe pymunk.pyglet_util.DrawOptions, que contém instruções de como desenhar o estado atual do espaço, e agora criamos uma instância no __init__ para utilizarmos depois.

Também criamos uma instância de pyglet.window.key.KeyStateHandler e à passamos para o método self.push_handlers, que nos permitirá verificar quais teclas estão pressionadas.

E finalmente, utilizamos pyglet.clock.schedule_interval para que nossa aplicação execute uma função periodicamente, a cada interval segundos. É no método update que iremos processar as teclas do teclado pressionadas e atualizar o estado de nossa simulação.

Temos todos os elementos necessários instanciados e configurados. Agora iremos tratar de desenhar nossas entidades na tela. Para isso, devemos sobrescrever o método on_draw, de pymunk.window.Window:

    def on_draw(self) -> None:
        self.clear()
        self.space.debug_draw(options=self.draw_options)

O primeiro passo é limpar a tela, com self.clear(), e em seguida, utilizamos debug_draw de nosso espaço simulado para desenhar as entidades.

E para atualizar o estado de nossa simulação, definimos update e chamamos self.space.step():

    def update(self, dt: float) -> None:
        self.space.step(dt=self.INTERVAL)

A função step atualiza nossa simulação, aplicando um passo de tempo dt. Utilizamos a mesma constante INTERVAL como maneira de simular as entidades em tempo real.

Caso se deseje fazer a simulação em slow motion, é possível passar frações desse valor para step (self.INTERVAL / 2, por exemplo). Também é possível multiplicar esse valor para deixar a simulação mais rápida em relação ao tempo real, porém ela perde em precisão.

É importante notar que o método update também recebe um argumento dt, que representa quanto tempo foi transcorrido desde a última chamada ao método. Isso se deve ao fato de schedule_interval não seguir o valor intervalo perfeitamente. Variações na utilização da CPU podem introduzir variações ao intervalo.

É bem tentador passar este dt diretamente à step, como forma de ter uma simulação bem sincronizada com o tempo real. No entanto, a recomendação da PyMunk é utilizar um intervalo constante em step. Isto não é um fator tão crucial em nosso caso, porém variabilidades no passo da simulação podem causar comportamentos inesperados, especialmente em relação ao cálculo de colisões.

Nesse momento, podemos executar nossa simulação:

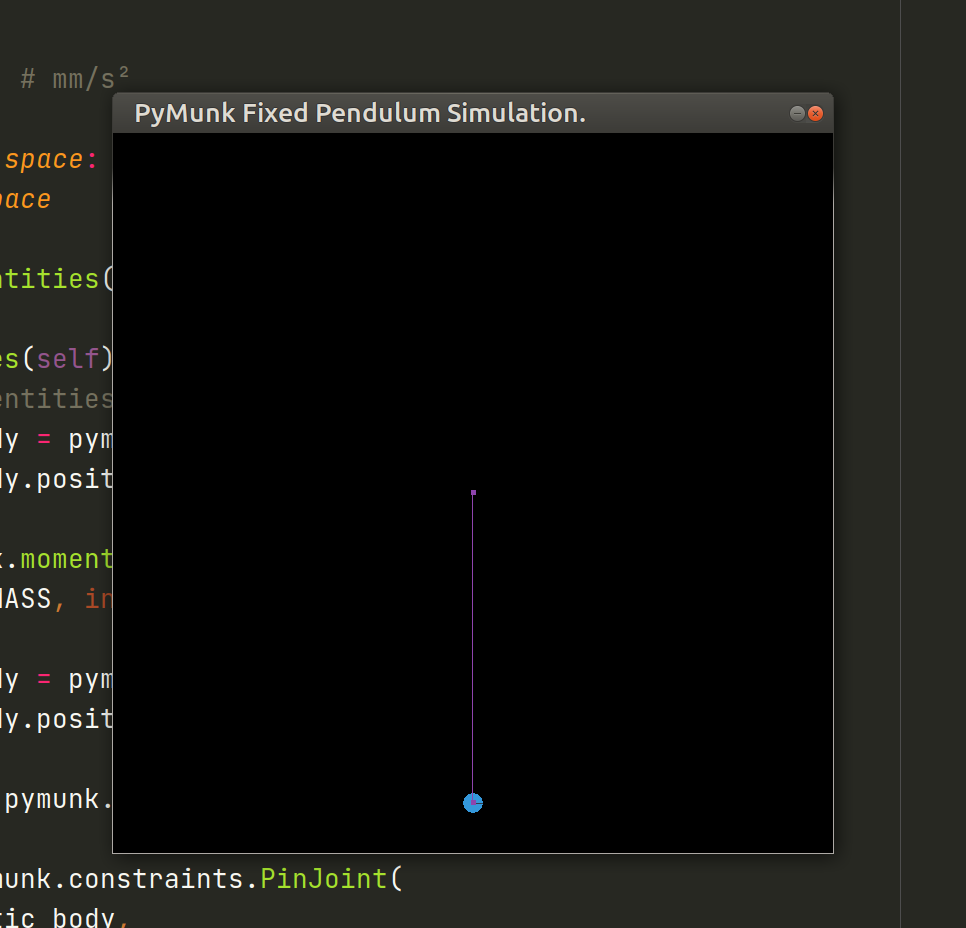
O pêndulo está sendo simulado, no entanto nada acontece! Isso ocorre pois ele está em estado de repouso e não há nenhuma força/aceleração sendo aplicada.

Para tornar esta simulação dinâmica, devemos extender nossa classe Pendulum:

    @property
    def vector(self) -> Vec2d:
        """Pendulum Vector, from Fixed point to the center of the Circle."""
        return self.circle_body.position - self.static_body.position

    def accelerate(self, direction: Vec2d):
        """Apply force in the direction `dir`."""
        impulse = self.FORCE * direction.normalized()
        self.circle_body.apply_impulse_at_local_point(impulse=impulse)

A propriedade vector é o vetor que representará o pêndulo, com origem no ponto estático e apontando ao centro do círculo. Os objetos da classe Body possuem o atributo position que é um Vec2d, que já suporta operações entre vetores, então basta subtrair a posição do static_body da posição do circle_body.

O método accelerate aplicará uma força ao círculo do pêndulo. Recebemos um argumento direction para determinar a direção da força que será aplicada.

A constante FORCE é uma grandeza escalar. Para transforma-la em um vetor, normalizamos o vetor direção, como forma de garantir que ele terá módulo 1, e então multiplicamos pela constante.

Chamo este vetor de impulse, ou impulso, pois trata-se de uma força instantânea. Esta é uma distinção importante para a pymunk, já que esta possui dois métodos principais de aplicar uma força a um corpo:

• apply_force_at_local_point
• apply_impulse_at_local_point

O método apply_force_ aplica uma força constante, que continuará afetando o corpo até que esta seja cessada, como por exemplo um motor de um carro. Já o apply_impulse_, aplica esta força de maneira instantânea, alterando a velocidade e direção do corpo apenas no próximo step, como um projétil sendo atirado de um canhão, por exemplo.

Há também os métodos apply_force_at_world_point e apply_impulse_at_world_point. A diferença é a maneira como são processadas as coordenadas de referência do vetor força em relação ao objeto. No caso de local_point, as forças são aplicadas como se tivessem sendo geradas a partir do próprio objeto, como por exemplo um sistema de propulsão. Já world_point, é como se as forças fossem originadas externamente.

Com accelerate definido, a ideia é permitir aplicar esta força ao pêndulo de acordo com o que for pressionado no teclado:

    def _handle_input(self):
        if self.keyboard[key.LEFT]:
            direction = self.model.vector.rotated_degrees(-90)  # CW
            self.model.accelerate(direction=direction)
        elif self.keyboard[key.RIGHT]:
            direction = self.model.vector.rotated_degrees(90)  # CCW
            self.model.accelerate(direction=direction)

    def update(self, dt: float) -> None:
        self._handle_input()
        self.space.step(dt=self.INTERVAL)

Para isto, crio o método _handle_input, que será chamado no método update, antes de atualizar o estado da simulação.

self.keyboard é uma instância de KeyStateHandler, que após ser passado como argumento de self.push_handlers, funciona como um dicionário indicando quais teclas estão pressionadas naquele instante. Utilizamos este atributo para verificar se as teclas Direita (right) ou Esquerda (left) estão selecionadas e aceleramos o pêndulo caso estejam.

A ideia é aplicar uma força no sentido horário, qdo a tecla esquerda é pressionada, e anti-horário, qdo a direita é pressionada. Como o circulo do pêndulo segue uma trajetória circular, é preciso fazer com que a direção da força aplicada seja sempre perpendicular ao vetor do pêndulo, como mostra o diagrama a seguir:

Para realizar isto, acessamos o vetor através de self.model.vector e chamamos o método rotated_degress() para rotacionar ele em -90 ou 90 graus, dependendo do sentido. Não há de se preocupar com o módulo deste vetor, pois ele é normalizado na função accelerate.

Com isso, nossa simulação está completa. É possível fazer o pêndulo se mover:

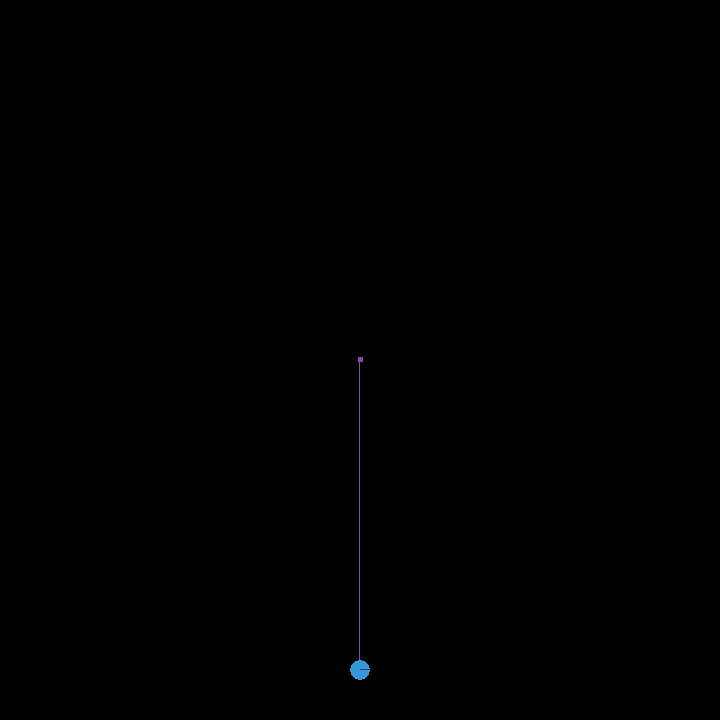
O código completo desta simulação está disponível neste GIST: